

The rules of differentiation (product rule, quotient rule, chain rule, ) have been.
#Limit chain rule how to
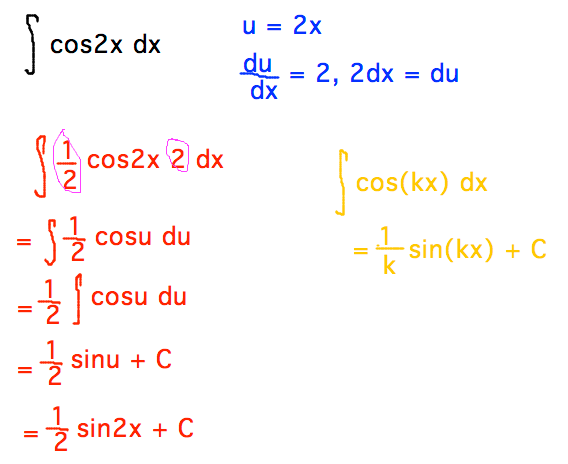
What is the chain rule in differentiation?.The following operations can be performedĢ*x - multiplication 3/x - division x^2 - squaring x^3 - cubing x^5 - raising to the power x + 7 - addition x - 6 - subtraction Real numbers insert as 7.
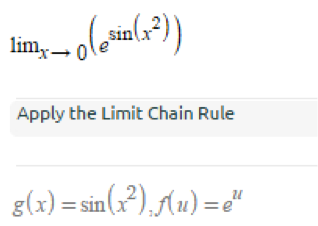
The error function erf(x) (integral of probability), In this case, f(x) is called the outer function, and. Hyperbolic cosecant csch(x), hyperbolic arcsecant asech(x), In calculus, Chain Rule is a powerful differentiation rule for handling the derivative of composite functions. The above form is called the differentiation of the function of a function. Secant sec(x), cosecant csc(x), arcsecant asec(x),Īrccosecant acsc(x), hyperbolic secant sech(x), Other trigonometry and hyperbolic functions: For example, sin(x) is a composite function because it can be constructed as f(g(x)) for f(x)sin(x) and g(x)x. This is to allow us to notice that when we do differentiate the second term we will require the chain rule again.

In other words, it helps us differentiate composite functions. Hyperbolic arctangent atanh(x), hyperbolic arccotangent acoth(x) The chain rule states that the derivative of f(g(x)) is f'(g(x))g'(x). Hyperbolic arcsine asinh(x), hyperbolic arccosinus acosh(x), These rules, for example, allow you to calculate the derivative of any rational ( ratio of two polynomials) function. In this article, we will calculate the derivative of cos x and also discuss. Hyperbolic tangent and cotangent tanh(x), ctanh(x) It can be derived using the limits definition, chain rule, and quotient rule. The hot glowing gas of a star radiates energy according to the function E s T 4.If T is a function of the radius of the star, use the Chain Rule to find a formula for dE/dr. Hyperbolic sine sh(x), hyperbolic cosine ch(x), Solution using the meaning of composed functions, the chain rule and the given data: 4. Sinus sin(x), cosine cos(x), tangent tan(x), cotangent ctan(x)Įxponential functions and exponents exp(x)Īrcsine asin(x), arccosine acos(x), arctangent atan(x), the derivative of y with respect to x, is equal to the limit as delta x approaches zero of change in y over change in x. The modulus or absolute value: absolute(x) or |x| But how do we actually go about proving it Well we just have to remind ourselves that the derivative of y with respect to x. Detailed solution for the specified methods:.First Remarkable Limit (Sandwich Theorem).This rule is called the chain rule and has a variety of applications. 3) You could multiply out everything, which takes a bunch of time, and then just use the quotient rule. In this module, one of the most important of the differentiation rules of this course is developed which will allow us to find derivatives of the compositions of functions. 2) Use the chain rule and the power rule after the following transformations. The Limit One-Sided Limits Limit Properties Computing Limits Infinite Limits Limits At Infinity, Part I. Limits of rational fractions at the end point Many functions are created through composition of other functions.Limits of rational fractions at infinity.


 0 kommentar(er)
0 kommentar(er)
